Fitting 13C breath test

R
advanced
nonlinear fit
nlme
Stan
Author

Dieter Menne

Published

November 18, 2024

Raw data of breathtest time series

Summary

Time series from 13C breath test recordings are used as a surrogate indicator for gastric emptying. Gastric emptying half time t50 is computed by fitting the series with an exponential beta or a Gamma function. Often, records are too short to obtain stable estimates of the trailing part. One can easily get unrealistic emptying times when single curves are fitted (Ghoos et al. (1993), Maes et al. (1998)).

Population methods can come to the rescue. When these fail, Bayesian methods provide a robust approach to non-linear curve fitting.

The methods described here are implemented in packages breathtestcore and breathtestshiny, and can be tested online here

Zipped source files and data

Single curve fit

Single curves fits - the standard method used in breath test evaluation - can be computed with function nlsList from package nlme. The exponential beta ExpBetafunction is defined in package D13CBreath; use devtools::install_github("dmenne/d13cbreath") to install. To compute the half-emptying time t50, use function t50BluckCoward or t50Maes from the same packages. The exponential beta function is parameterized as k = 1/tempt, because fits are close to normal distribution when k is estimated instead of tempt. The dose is fixed to 100 (mg); with this choice, factor m can be interpreted as the fraction of 13C metabolized over the complete extrapolated emptying curve.

Click for code 
start <- c(m = 30, k = 0.01, beta = 1.8)
d_nls <- nlsList(
  PDR ~ ExpBeta(Time, 100, m, k, beta) | BreathTestRecordID,
  data = d, start = start
)
Warning in log(.expr7): NaNs wurden erzeugt
Warning in log(.expr7): NaNs wurden erzeugt
Warning in log(.expr7): NaNs wurden erzeugt
Warning in log(.expr7): NaNs wurden erzeugt
Warning: 4 Mal denselben Fehler abgefangen in qr.default(.swts * gr):
NA/NaN/Inf in externem Funktionsaufruf (arg 1)
Click for code 
cf_nls <- coef(d_nls) %>%
  rownames_to_column("BreathTestRecordID") %>%
  mutate(
    method = "nls",
    t50BW = t50BluckCoward(.),
    t50Maes = t50Maes(.)
  )
cf_nls
   BreathTestRecordID  m      k beta method t50BW t50Maes
1                P435 48 0.0056  1.6    nls  31.2     187
2                P436 54 0.0054  1.6    nls  30.4     190
3                P443 64 0.0123  1.9    nls  25.4      97
4                P444 34 0.0060  2.0    nls  55.0     201
5                P446 NA     NA   NA    nls    NA      NA
6                P455 NA     NA   NA    nls    NA      NA
7                P457 13 0.0107  3.9    nls  87.2     170
8                P475 NA     NA   NA    nls    NA      NA
9                P485 26 0.0094  1.4    nls   8.7     100
10               P487 20 0.0100  2.1    nls  39.5     127
11               P489 NA     NA   NA    nls    NA      NA
12               P496 33 0.0084  2.3    nls  55.6     161

With single curve fits, the underlying function nls does not produce valid fits for 4 records. Packages like MathPad or Matlab might give solutions, but these are most likely associated with huge errors of the coefficients. R uses a much more conservative approach and returns NA as a feature, not a bug (Douglas Bates, personal communication).

Population fit with nlme

The population fit with function nlme from package nlme uses the full information from all curves, giving more stable estimates from “borrowing strength” providing guidance in critical cases such as P443. However, fitting all data with nlme fails; by trial-and-error one can find out that three records must be excluded to force convergence:

Click for code 
d_part <- d[!(d$BreathTestRecordID %in% c("P446", "P489", "P455")), ]
d_nlme <- nlme(PDR ~ ExpBeta(Time, 100, m, k, beta),
  data = d_part,
  fixed = m + k + beta ~ 1,
  random = m + pdDiag(k + beta) ~ 1,
  groups = ~BreathTestRecordID,
  control = nlmeControl(pnlsTol = 0.05),
  start = start
)
Warning in log(.expr7): NaNs wurden erzeugt

In addition to removing the three offending records, the value of pnlsTol has been increased from its default of 0.001. Always use the smallest value that leads to convergence; trial-and-error is required; function nlme_gastempt in my package gastempt automatically adjusts pnlsTol until convergence. Values above 0.5 are dubious and indicate that the results might not be trusted.

The computed coefficients from nlme and derived quantity t50 (emptying half time in minutes):

Click for code 
cf_nlme <- coef(d_nlme) %>%
  rownames_to_column("BreathTestRecordID") %>%
  mutate(
    method = "nlme",
    t50BW = t50BluckCoward(.),
    t50Maes = t50Maes(.)
  )
cf_nlme
  BreathTestRecordID  m      k beta method t50BW t50Maes
1               P435 48 0.0057  1.6   nlme  31.7     185
2               P436 53 0.0055  1.6   nlme  30.9     188
3               P443 64 0.0123  1.9   nlme  25.3      97
4               P444 34 0.0061  2.0   nlme  55.3     199
5               P457 16 0.0085  3.1   nlme  85.8     190
6               P475 49 0.0031  2.7   nlme 193.0     479
7               P485 26 0.0094  1.4   nlme   8.9     100
8               P487 20 0.0099  2.1   nlme  39.3     128
9               P496 33 0.0083  2.3   nlme  55.3     162

Bayesian fit with Stan

Stan is a comprehensive Open-Source package for Bayesian analysis. For a different evaluation of breath test data using Bayesian methods, see also Bluck et al. (2011).

The following Stan model was used:

# All parameters have hard lower limit at 0
m ~ normal(20,25);
beta ~ normal(2,0.4);
k ~ normal(0.0015,0.001);
sigma ~ cauchy(0,5);

for (n in 1:N){
  rec = Record[n];
  mn  =  m[rec];
  kn = k[rec];
  ktn = kn* Time[n];
  betan = beta[rec];
  # Dose fixed to 100
  pdr = 100*mn*kn*betan*exp(-ktn) * pow(1 - exp(-ktn),(betan -1));
  PDR[n] ~ normal(pdr,sigma);
}

Data are passed to Stan as a list.

Click for code 
data <- list(
  N = nrow(d), NRecord = NRecord, Record = d$Record,
  Time = d$Time, PDR = d$PDR
)
Click for code 
str(data, vec.len = 1)
List of 5
 $ N      : int 483
 $ NRecord: int 12
 $ Record : int [1:483] 1 1 ...
 $ Time   : num [1:483] 0.5 8.7 ...
 $ PDR    : num [1:483] 3.4 7.5 ...

The number of data N and the number of records NRecord for indexing of the parameter block must be passed to allocate the data vectors

data{
  int<lower=0> N; # Number of data
  int<lower=0> NRecord; # Number of records
  int<lower=0> Record[N]; # From BreathTestRecordID
  real<lower=0> Time[N];
  real<lower=-30> PDR[N];
}

These following parameters are computed, one for each gastric emptying time curve (=record):

parameters{
  real <lower=0> m[NRecord];
  real <lower=0> k[NRecord];
  real <lower=0> beta[NRecord];
  real <lower=0> sigma;
}

Stan model compilation and running needs a few minutes, therefore the result is explicitly cached as follows:

Click for code 
stanCache <- "BreathTestStan1.rdata"
if (!file.exists(stanCache)) {
  mr.stan <- stan("BreathTestStan1.stan",
    seed = 123, chains = chains,
    iter = 200, data = data
  )
  save(mr.stan, file = stanCache)
} else {
  load(stanCache)
}

4 chains with random initial values are run, each with 100 warmup iterations at a total of 200 iterations.

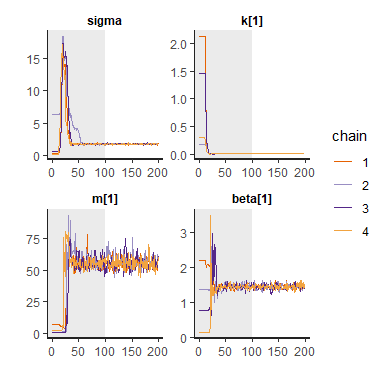
Stan diagnostics

The left part of the panels with gray background indicate the warmup (“burn-in” in non-Gelman based literatur) range of 100 iterations. Stan has converged after about 40 iteration for all chains

Click for code 
stan_trace(mr.stan, pars = c("sigma", "k[1]", "m[1]", "beta[1]"), inc_warmup = TRUE)

Traceplot of sigma and parameters of the first record

Predictions

Click for code 
dict <- unique(d[, c("BreathTestRecordID", "Record")]) %>%
  mutate(
    BreathTestRecordID = as.character(BreathTestRecordID)
  )

cf_stan <- tibble(
  m = get_posterior_mean(mr.stan, pars = "m")[, chains + 1],
  k = get_posterior_mean(mr.stan, pars = "k")[, chains + 1],
  beta = get_posterior_mean(mr.stan, pars = "beta")[, chains + 1],
  stringsAsFactors = FALSE
) %>%
  mutate(
    method = "Stan",
    Record = 1:n(),
    t50BW = t50BluckCoward(.),
    t50Maes = t50Maes(.)
  ) %>%
  left_join(dict, by = "Record") %>%
  select(BreathTestRecordID, m, k, beta, method, t50BW, t50Maes)
# Combine all results
cf_all <- rbind(cf_stan, cf_nlme, na.omit(cf_nls))

min <- seq(0, 240, by = 5)
# Separate overlapping curves
offset <- c(nlme = 1, nls = 0, Stan = -1)
pred <- cf_all %>%
  rowwise() %>%
  do(tibble(
    method = .$method,
    BreathTestRecordID = .$BreathTestRecordID,
    min = min,
    PDR = ExpBeta(min, 100, .$m, .$k, .$beta) + # Slightly shift
      0.3 * offset[.$method]
  ))

ss <- apply(table(pred$BreathTestRecordID, pred$method), 1, sum)
partial <- names(ss[ss != max(ss)])

colors <- setNames(
  scales::hue_pal(h = c(0, 360) + 15, c = 100, l = 55, h.start = 0, direction = 1)(3),
  c("nlme", "nls", "Stan")
)

plot_fits <- function(d, pred, subset = NULL) {
  ggplot(data = d, aes(x = Time, y = PDR)) +
    geom_point(size = .8, color = "gray") +
    geom_line(data = pred, aes(x = min, y = PDR, color = method)) +
    facet_wrap(~BreathTestRecordID) +
    scale_x_continuous(breaks = seq(0, 250, by = 100)) +
    scale_color_manual(values = colors)
}
Click for code 
plot_fits(d, pred)

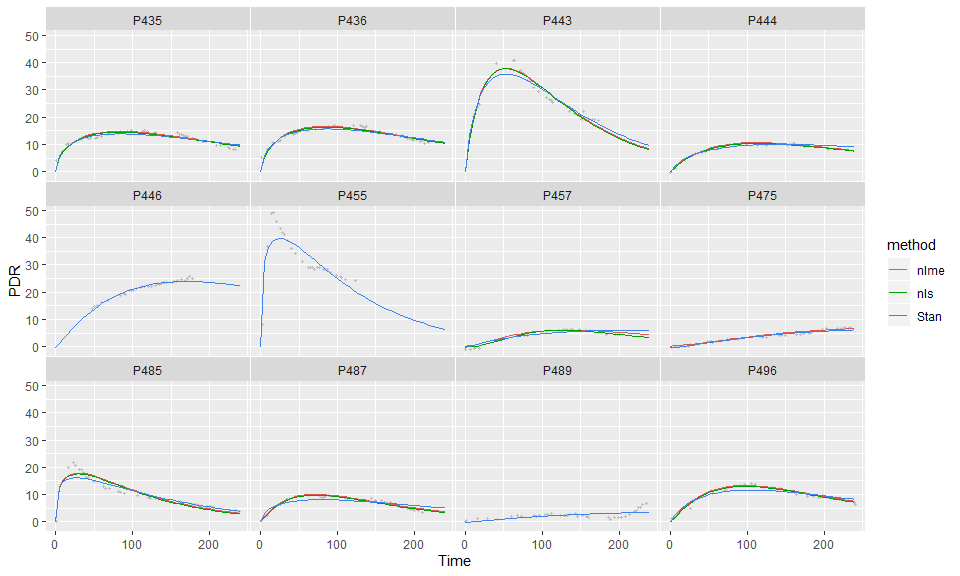
All fits and raw data (gray). To better separate overlapping curves, these are vertically shifted against each other by 0.5 units.
  • Population fits and Bayes fits are very similar. Bayes and nlme (population) fits do not provide an advantage when the nls fit converges.
  • Since single-curve fits are often reliable for recordings with the half-emptying-time included. In these cases, the fit is well defined with only little correlation between the parameters.

Things can go wrong

  • For three record (P446, P455, P489), only Stan gives valid fits.
  • For one record (P475), Stan and nlme give valid fits
Click for code 
d_p <- d[d$BreathTestRecordID %in% partial, ]
pred_p <- pred[pred$BreathTestRecordID %in% partial, ]
plot_fits(d_p, pred_p)

Records for which single fits do not give valid results
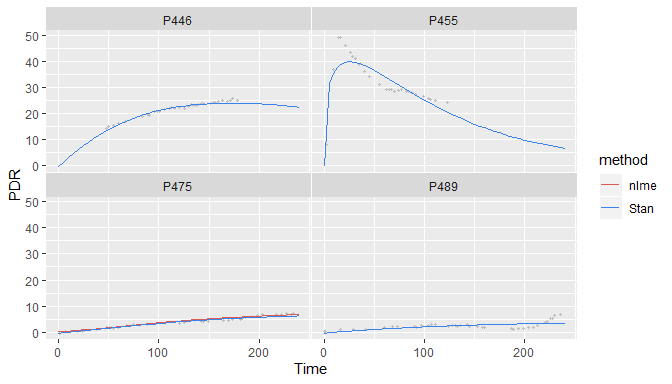
  • In extreme cases, only the Bayesian method returns an estimate.
  • The self-corrected estimate of t50 following Bluck-Coward is definitively too low.
  • The estimate of t50 following Maes/Ghoos is too high for some cases (> 10 h).
  • The fact that curves can be fitted does not mean that the fits give medically meaningful results.
Click for code 
knitr::kable(
  cf_all[
    cf_all$BreathTestRecordID %in% partial,
    c("method", "BreathTestRecordID", "m", "k", "beta", "t50Maes", "t50BW")
  ],
  row.names = FALSE, digits = c(0, 0, 1, 4, 1, 1)
)
Table 1: Estimated parameters from Stan for the three records with invalid fits. t50BW: t50 self-corrected after Bluck-Coward; t50Maes: t50 following Ghoos/Maes.
method BreathTestRecordID m k beta t50Maes t50BW
Stan P446 117 0.0042 2.1 298 88
Stan P455 61 0.0101 1.3 87 4
Stan P475 58 0.0025 2.3 537 187
Stan P489 40 0.0020 2.0 618 177
nlme P475 49 0.0031 2.7 479 193

Wagner-Nelson to the rescue??

A popular alternative when curve fitting does not work is the Wagner-Nelson method which uses non-parametric approaches for the initial slope. However, it makes a assumption about the terminal slope being the same for all subjects: k=0.01/min, 0.65/h. Since this assumption strongly affects the estimate of the half-emptying time, there is little justification to use the Wagner-Nelson method.

Citations

Bluck LJC, Jackson SJ, Vlasakakis G, Mander A (2011) Bayesian hierarchical methods to interpret the (13)c-octanoic acid breath test for gastric emptying. Digestion 83:96–107. doi: 10.1159/000316823
Ghoos YF, Maes BD, Geypens BJ, et al. (1993) Measurement of gastric emptying rate of solids by means of a carbon-labeled octanoic acid breath test. Gastroenterology 104:1640–1647.
Maes BD, Geypens BJ, Ghoos YF, et al. (1998) 13C-octanoic acid breath test for gastric emptying rate of solids. Gastroenterology 114:856–859.